Definition of Triangle
A polygon having three sides is called a triangle. Triangle has three sides and three angles and all these three sides are connected to each other. Where two sides are connected is called the vertex of the triangle. The main property of the triangle is the sum of three angles of a triangle equal to 180 degrees. A triangle of vertices A, B, and C are represented as ΔABC. Signboards and sandwiches are examples of triangles.
Shape of Triangle
Triangle is a two-dimensional shape surrounded by a coplanar of three straight lines. The point where any two straight lines intersect is called a Vertex. triangle has three vertexes and at each vertex, an angle is formed.
Different Parts of the Triangle
A triangle has many parts.it consists of three vertexes, three sides, and three internal angles. these different parts of the triangle are shown in the figure below:
From Above Figure
three sides of the triangle are
- (1) Side AB
- (2) Side BC
- (3) Side AC
three Internal Angles of the triangle are
- ㄥ1 =ㄥABC
- ㄥ2 =ㄥBAC
- ㄥ3 =ㄥBCA
Three Vertex of the triangle are
- Vertex A
- Vertex B
- Vertex C
Properties of triangle
In Geometry, Every shape has some unique property that distinguishes each other. In a similar way, Triangle has also some basic properties which are mentioned below:
- A triangle has three sides, three angles, and three vertexes.
- The sum of the angles of a triangle is 180 degrees.
- The exterior angles of a triangle always add up to 360 degrees.
- The sum of consecutive interior and exterior angles is supplementary.
- The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Similarly, the difference between the lengths of any two sides of a triangle is less than the length of the third side.
- The shortest side is always opposite the smallest interior angle. Similarly, the longest side is always opposite the largest interior angle.
Different Types of Triangle
Classification of triangles is done on the basis of Sides and Angle. On the basis of the length of the side, triangles are classified into three categories:
- Equilateral Triangle
- Scalene Triangle
- Isosceles Triangle
On the basis of the angle, triangles are classified into three categories these are:
- Obtuse Angle Triangle
- Acute Angle Triangle
- Right Angle Triangle
Now We shall discuss every type of triangle one by one
Equilateral Triangle
if all sides of a triangle are equal in length and also all three angles are equal then this type of triangle is called Equilateral Triangle. An Equilateral Triangle has been seen in the figure given below:
As shown in the above figure all the three sides of the triangle are equal in length.
Scalene Triangle
If all the three sides of a given triangle are not equal in length then this type of triangle is called Scalene Triangle. In Scalene Triangle all three angles are also not equal. A Scalene Triangle is shown in the figure below:From the above-given figure, it is clear that no sides are equal in length.Isosceles Triangle
if two sides of a triangle are equal in length then this triangle is called the Isosceles triangle. In the Isosceles triangle, angles in front of equal sides are also equal. An Isosceles triangle is shown in the figure given below:
In the above-given figure, the two sides AB and AC are equal in length. The angle in front of these two sides is also equal. ㄥABC =ㄥACB
Acute Angle Triangle
In a given triangle, if out of all three angles anyone's angle is less than 90 degrees then this triangle is called Acute Angle Triangle. The figure of the acute angle triangle is given below:
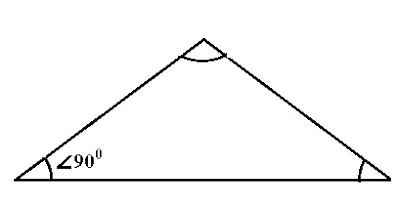
Right Angle Triangle
In a given triangle, if out of all three angles anyone's angle is equal to 90 degrees then this triangle is called the Right Angle Triangle. The figure of the Right angle triangle is given below:Obtuse Angle Triangle
In a given triangle, if out of all three angles anyone's angle is greater than 90 degrees then this triangle is called the Obtuse Angle Triangle. The figure of the Obtuse angle triangle is given below:In the above-given figure Angle, A is greater than 90 degrees.